噪声测定(1)

这个系列主要是记录一下最近新导入的噪声测定实验，预计包含原理和设备结构，也许会有数据分析。那么首先是关于噪声测定的一些基本知识。

C. Beenakker 和 M. Schçenberger指出，噪声是信号还是干扰取决于你想做什么。我们在进行物理实验的时候，常常穷尽各种手段去排除噪声的影响，因为它会限制物理量的精确度。然而，噪声中包含着大家忽略的信息。注意我们平时观测的物理量准确来讲应该称作平均值，其描述之后会提到。现实世界中的物质并不会固定在一个特定的状态，比如电流在流过材料是会产生随机波动，这个波动可以来源于涨落耗散，也可以来源于物质自身的特性。因此噪声本身也可以成为了解物性的工具之一，特别是我们常常说到的相变附近的强涨落。

那么我们首先考虑一般物理量是怎么测定的

$$<V>=lim_{T\rightarrow\infty}\int_{-T/2}^{T/2}V(t)dT$$

这代表了一定时间范围内的测量平均被认为接近真实值，在现实中我们的噪声通常呈现高斯分布(也叫正态分布)，即为

$$P(V)=\frac{1}{\sqrt{2\pi\sigma^2}}exp[-\frac{(V-<V>)^2}{2\sigma^2}]$$

σ是我们所谓的方差。在频率空间中，我们会讨论每个振动成分的强度，也就是哪个频率波动更大，这便是功率谱密度 Power spectral density。听起来复杂其实来源于傅里叶变换，比如我们考虑频域成分时

$$\tilde{V}(\omega)=\int_{-\infty}^{\infty}V(t)e^{-i\omega t}dt$$

那么PSD的定义便是

$$S_V(\omega)=\langle|\tilde{V}(\omega)|^2\rangle$$

那么需要注意这里PSD的量纲是V^2/Hz。在一个统计学的静态过程中，我们知道根据Wiener-Khinchin定理，PSD与自相关函数有关，因为我们认为一个动态平衡的状态可以认为是宽平稳过程，即

$$\Psi(t)=\langle V(t)V(t+\tau)\rangle$$

则我们可以认为PSD是自相关函数的傅里叶变换实部，因为频率正负(即相位反转)并不会改变我们测定电压的特性。

$$S_V(\omega)=4\int_0^{\infty}\Psi(\tau)cos\omega\tau d\tau$$

这里需要详细讨论自相关函数的物理意义，Ψ表示经过特定时间τ之后波动的残留成分，因此其描述了随机涨落中的固定成分，即系统自身涨落耗散的平均值随时间变化，最终我们明白Ψ描述的对象是电子在固体中流动的动力过程。

在实际测量中，我们可以测得系统的PSD，因此只需要通过傅里叶变换，即可得到这个系统的自相关函数，从而了解其涨落的信息。所以，当假设τ的间隔为0时，我们计算出来的自相关函数便是测量的方差，也就是我们的测量摇动。因为我们从测量数值中减去均值以后即可得到如下结果(注意之前所说的自相关函数和PSD互为傅里叶变换)

$$\sigma^2+\langle V(t)\rangle^2=\langle V(t)^2\rangle=\langle V(t)V(t+0)\rangle=\int_0^\infty S_V(f)df=\Psi(0)$$

我们先跳过如何具体计算PSD，因为这涉及到测量设备的问题。接下来看几个典型的噪声实例和其对应的具体原因。

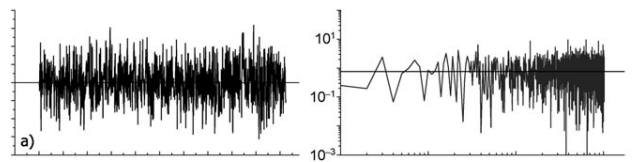
如上左图(x轴为时间t，y轴为测量值)所示，这是乱数生成模拟出的噪声，即为一种完全随机的信号，通称为白噪声(最常见的例子是热噪)。考虑到这种完全随机涨落信号在任何(！！)时间点都是随机的，功率谱在高频处会呈现发散的样貌。这是因为无论将采样率如何提升，白噪都是随机变化，说明白噪是无限变化的，而这对应了高频领域的无限功率。反之，在低频领域功率谱S会收敛为一个定值，因为其在每单位带宽的功率是相等的。所以我们看到右图(x轴为频率的对数，y轴为对应功率)的功率谱为一条相对平坦的直线。

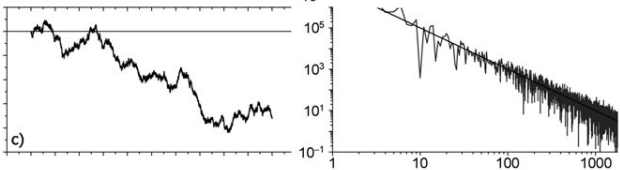
接下来看这张图，这是一个典型的布朗运动(Random walk)所产生的噪声。其功率谱具有S~1/f^2的关系。这表明噪声的高频功率是收敛的，而低频是趋近于无限大的。我们试想一下原因，在数步程度内(也可以说是短时间内)的布朗运动呈现出在某点周围的随机运动，因此我们测量得到的方差相对有限，对应上述公式不难发现在这样一个时间平均下功率谱也是有限(收敛)的。然而我们把时间范围假设拉伸到足够大的时候，我们所得到的结果对应了低频噪声，而由于布朗运动的随机性，其一定会偏离最初的起点，那么时间越长偏离程度越大，很容易想到方差在f=0处发散。在这种情况下功率谱各点之间的强度是相关联的。

上述两个例子对应了完全理想状况下的噪声，而在现实中我们得到的结果往往是介于二者之间的，即功率谱既显示出我们的系统在有限的时间范畴下发生了某些涨落，而在高低频极限时发散。其中既包含快速涨落，也包含了缓慢的变化趋势。这种噪声的功率通常趋近于频率的倒数1/f，所以被称为1/f噪声，也有人称其Excess噪声和Flicker噪声。1/f噪声可以代表一个长期的过程，因为当某一时刻发生了波动时，其功率就能被留在功率谱相对应的频率上。这种噪声能出现在各种各样的领域，比如人类的心跳，天文学的测光光变曲线甚至是巴赫协奏曲的响度和音调波动。当然，我们现在明白由于1/f噪声包含了大量不同时间范围的信息，因此其实是由于数学上的巧合最终呈现出1/f的曲线。