不得不感叹一下天才就是天才,我好不容易想了半年的点子Liang Fu教授早在2015年就把理论完成了,同研究室毕业的学长Onishi Yugo又和Fu在去年把应用的理论完成了。简直可以说帮我把路铺得不能再平。每次看到天才们就会萌生退坑保平安的想法。
那么回归正题,最近由于在考虑非线性霍尔效应的应用技术,那么作为非线性霍尔效应核心的浆果(误)曲率偶极子自然是重中之重。由于这个总结准备拿去给后辈讲课,所以我争取用比较浅显的方式从头开始讲起。
在明白偶极子这个较为复杂的概念前,我们需要先明白Berry曲率究竟是什么,以及对称性的重要性在哪里。天才般的先贤(?)们为大家整了一个最为简单的描述方式。
首先,我们考虑一个趴在平面上的箭头。我们规定这个箭头只能平移不能旋转,那么不难发现不论怎么去挪动这个箭头,它的指向永远是固定的。
好,接下来让我们把空间稍微扭曲一下,这样我们的平面就变成了一个曲面。和刚才一样我们让箭头只平移不旋转,从图中的点1出发沿路径平移一周回到点1。结果发生了什么?明明我们没有做任何旋转操作,箭头的方向却产生了变化,这个方向的变化便是几何相位。
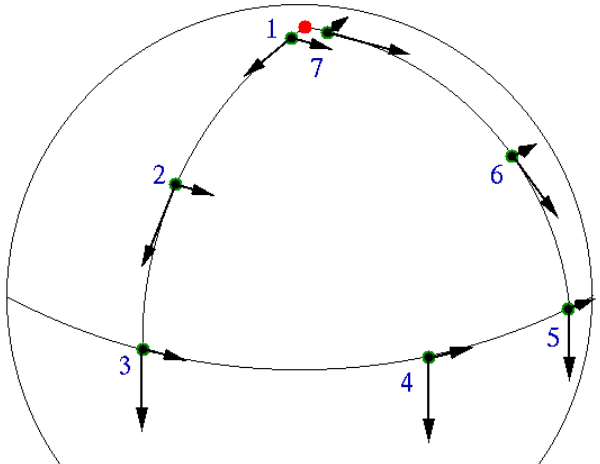
回到物理中来,我们知道电子在晶体中运动的时候,为了考虑电子的运动模式通常大家会在动量空间内来看待问题。电子通常用波函数描述,即为
$$\Psi=Ae^{ikx}$$
这个形式,由于我们在动量空间下,所以自变量(对应真实世界中的位移)便是波矢k。假设电子是和刚才那个箭头一样有朝向的(确实可以有,就是运动方向),我们把刚才的箭头比做电子,球面比做k空间的费米面,让电子沿着费米面某个路径运动一周。因为在晶体中k同样具有周期性,因此这对应了真实世界中电子从一个晶格移动到下一个的实际过程。
那么我们不难想到,电子的朝向在运动中发生了改变,这个改变体现到波函数上便是
$$\Psi= Ae^{i(kx+\phi)}$$
即相位发生了改变,放到实际中来说就是电子的运动路线被什么玩意强行掰弯了(x。所以我们可以说,这个相位使得动量空间不再平坦,而是产生了某些空间上的弯曲,而描述这个弯曲程度的量便是我们的主角,Berry Cuvature Ω(k)。
【接下来的内容包含公式推导,看不懂不影响内容】
不过要讨论实际上的Berry曲率,我们还是要从物理的角度来说明为何布洛赫电子可以在运动中获得额外的相位。让我们跟随肖迪教授的综述来简单了解一下纯理论角度的电子世界[1]。
我们之前提到,电子在费米面巡回一周这个行为。需要约定,这个过程中不能有任何其它原因的干扰巡回行为,否则我们看到的现象就无法保证来源于相位差本身(这是为了理论上的严谨,现实中Berry曲率相关的现象具有相当强的抗干扰性)。
什么情况能隔绝外界干扰呢?这便是绝热循环演化,它保证了系统在没有能量交换的情况下准静地发生时间演化。从薛定谔方程出发
$$i\hbar\frac{\partial}{\partial t}\psi(t)=H\psi(t)$$
根据量子绝热理论(Kato,1950),初始状态为本征固有值的波函数在随后的时间会一直处于该状态下的时间演化。那么对于电子而言,它能被改变的只有波函数的相位这一个值,因为其它状态已经被固定。因此对任意时间的波函数可以被认为
$$\psi_n(t)=\\e^{i\gamma_n(t)}exp[-\frac{i}{\hbar}\int_0^t dt’ \epsilon_n(R(t’))](nR(t))$$
在这里nR(t)代表某个本征态。我们为了方便,可以把第二项来源于动力演化的成分简单设为iθ。如果将上述波函数带入薛定谔方程,再乘以波函数的左矢,便可以得到
$$\frac{d}{dt}\gamma_n(t)=i\langle nR(t)|\frac{d}{dt}|nR(t)\rangle$$
接下来计算就简单多了,我们对整个等式进行对整个循环演化的时间积分便可以得到
$$\int d\gamma_n=\int id\langle nR(t)|nR(t)\rangle$$
左侧积分非常简单,即为γn,右侧积分由于是对整个循环积分得到的结果,所以实际的积分范围应为整个循环路径C,即为
$$\gamma_n=\int_C i\langle nR(t)|\frac{\partial}{\partial R}|nR(t)\rangle dR$$
接下来为了描述方便,我们定义
$$A_n=\langle nR(t)|\frac{\partial}{\partial R}|nR(t)\rangle$$
这里的An代表了Berry connection,代表了电子运动路径起点和终点的闭合。这里依然要强调电子处于晶体之中,因此终点便是进入下一个布里渊区也就是下一个晶格周期。话说回来,由于电子的运动满足规范场变换,因此通常而言运动带来的相位γn会被规范场的相位在路径C上抵消掉。但是,我们在这里考虑的却是一个绝热循环,这下问题就来了。电子巡回一周回到最初的状态时,规范场带来的相位必然是2π的整数,否则就无法回到原点(因为e^2inπ=1)。好了,我们发现波函数在巡回一周以后多出来个相位γn。通过计算过程可以得出它具有下列性质
γn规范不变,γn的取值与闭环路积分的路径C密切相关,γn和时间演化无关。
因此可以说,这种相位差是物质内禀的性质,与外界无关。如果我们利用格林定理即可发现
$$\gamma_n=\int_SdS \Omega_n(k)$$
这里\(\Omega_n=\nabla_k\times A_n(k)\),而\(\Omega_n\)是我们所说的Berry Curvature。这个式子看上去和磁通量的形式完全相同,因此我们得出结论,Berry曲率可以被认为是物质内部自发形成的假想磁场,而Berry connection可以被认为是potential vector一样的存在。
我们发现电子这个被改变的相位源于动量空间的路径本身,与外界无关。接下来简单说一下Berry曲率函数和对称性的关系,这是我们的核心之一。由于这里只是纯数学计算,因此我们就不展现详细步骤,根据京都大学越野幹人教授的讲义[2],我们明白:
1、仅保持时间反演对称时,Berry曲率为奇函数。
2、仅保持空间反演对称时,Berry曲率为偶函数。
3、同时保持上述两种对称时,不存在Berry曲率。
【题外话:什么时间、空间反演对称?
时间反演对称用白话说就是把你正着走的影片倒放一下,如果影片里除了你是反着走的其他东西都没变化那就是时间反演对称。比如,你往前走的时候有一只鸟飞起来了,那倒放你走路的视频鸟就是落下来的,对于这段视频来说时间显然不对称。对物质来说时间不对称体现在电子的正负运动方向是否表现相同,其余就不赘述了。
空间反演对称相对更好理解一些,说白了就是把一个物体的坐标全都加上个负号,如果加完以后物体的样子和以前一样,那就是对称的。】
到目前为止,凝聚态物理界绝大多数关于Berry曲率的研究,都集中在时间反演对称破缺的情形下。因为根据公式的推导,我们知道
$$\gamma_n=\int_SdS \Omega_n(k)$$
也就是说,时间反转被打破时,Berry曲率\(\Omega_n(k)\neq -\Omega_n(-k)\),上式积分结果必然不为0,代表系统一定会出现有限的Berry相位。这种情况下,系统相当于内部自发出现了一个和磁场效果一样的东西。我们知道对金属z轴方向施加磁场以后,x方向的电流会引发y方向的电压,这便是霍尔效应(下图)。
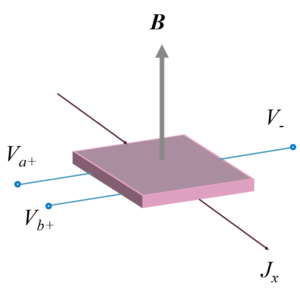
而在有限Berry相位的系统中,由于电子在运动中会自发的获得额外相位,因此其运动方向即使不存在外部磁场,也会被改变,从而出现零场霍尔电压,这便是赫赫有名的反常霍尔效应。不过,在这篇文章中时间反演对称破缺带来的Berry相位并不是重点,因此我们一笔带过,接下来才是重点。
在2010年时,J. E. Moore考察了自1990年来被提倡的“现代极化理论”,即如果空间反演对称发生破缺,则系统同样会产生有限的Berry曲率。Moore提出,在GaAs这样无旋光性物质的量子阱中,空间反演对称破缺带来的Berry phase可以引发直流性质的光电流[3](这里得提一句Moore所说的光电流并非光电效应,而是类似旋光性带来的光电流)。而在2015年时,Liang Fu提出这种光电流中不仅存在直流成分,还存在输入电流的二次谐波成分,这奠定了未来非线性霍尔效应的基础[4]。我们先不谈高深的理论(毕竟我自己都没看太懂),而是从现象论角度出发来看看。
请注意之前对Berry曲率性质描述是标红的部分,当空间保持反演对称时,Berry曲率函数为偶函数。这意味着在先前提到的时间反演对称破缺下,Berry曲率为偶函数,即\(\Omega_n(k)=\Omega_n(-k)\)。我们发挥空间想象力假设能带在\(k_x-k_y\)平面考虑最简单的自由粒子能带分布\(\epsilon=\frac{\hbar^2(k_x^2+k_y^2)}{2m}\),能带上的Berry曲率分布显然应该长成下图左侧这样。在某个能级的xy平面上所有状态的曲率一致,这样的结构被称作Berry单极子,它就像一个电荷产生的电场一般,曲率向外发散或者向内吸收。
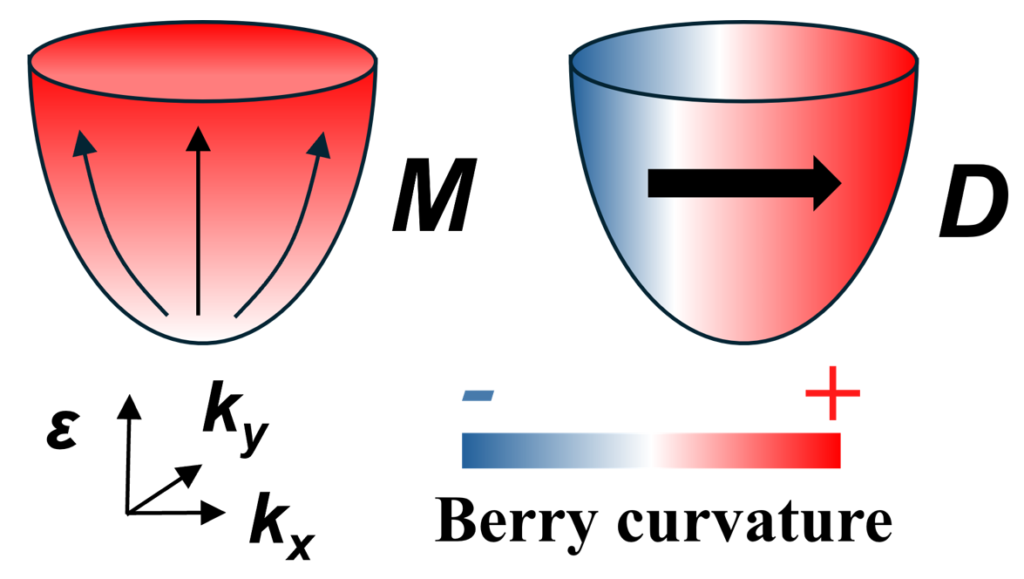
接下来,让我们想想时间反演对称性存在,空间反演对称性破缺的情况。依然考虑自由粒子能带分布\(\epsilon=\frac{\hbar^2(k_x^2+k_y^2)}{2m}\)。这时,\(\Omega_n(k)= -\Omega_n(k)\),那么对于Berry相位的积分而言,正常情况下显然所有状态的曲率之和为0(想不明白就类比一下sin函数+π到-π范围的积分),具体可以参照下图最左侧。但是吧,总有那么点不正常的情况,这便是非平衡态。对于它的平衡态而言,能带从上往下看肯定是一个圆心为原点的圆。如果对这个系统的x方向加个电流,则能带在x方向上就会如下图所示产生偏移,就如同下图中间所展示的样子。这下问题来了,本来是奇函数的Berry曲率连奇函数都不是了,再来看它的相位积分显然不再为零。这便是上图以及下图右侧所展示的Berry曲率偶极子。之所以称为偶极子是因为其一侧曲率之和为负,另一侧为正。到此,我们理解了空间反演破缺会带来Berry曲率偶极子这一事实。
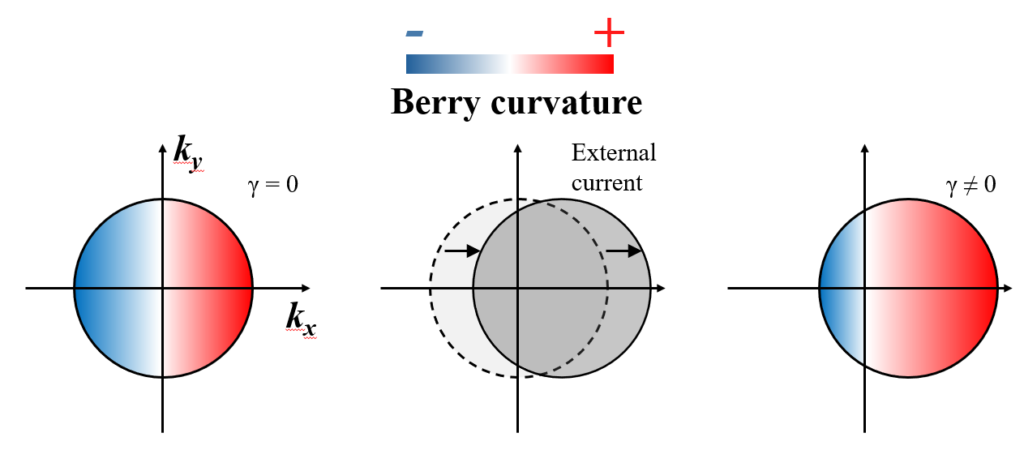
在我看来,Berry曲率偶极子是现代铁电极化转向拓扑的核心观点,因为之后的一系列非线性现象,最终都是围绕Berry曲率偶极子所展开的。那么,之后有空我会继续记录Berry曲率偶极子带来的千奇百怪的非线性现象。
Ref:
[1] D. Xiao et al., Rev. Mod. Phys. 82, 1959 (2021)
[2] 越野幹人 物性研究電子版 7, 2.072210 (2018)「トポロジカルなバンド構造と物性物理」
[3] J. E. Moore and J. Orenstein Phys. Rev. Lett. 105, 026805 (2021)
[4] I. Sodemann and L. Fu Phys. Rev. Lett. 115, 216806 (2015)]
发表回复