本文分为以下几个部分:
- 太阳及观测方法
- 法布里佩罗干涉仪
2.1 多光束干涉
2.2 点扩散单色光的干涉
2.3 平行白光的干涉 - 诱导透射滤镜
注:公式推导参考http://staff.ustc.edu.cn/~chunhua/3-05.pdf
1. 太阳及观测方法
太阳,炽烈且明亮,而在灿烂的白光中又隐藏着许多有趣的特征。让我们从太阳的大气层内说起:太阳的大气层被分为三部分,从外到内分别为日冕,色球层和光球层。它们的温度依次减,但亮度却是日冕最暗,光球最亮。我们看到的太阳通常指光球层,光球层中存在强烈的等离子气体对流,一个个对流柱被太阳磁场所约束形成了所谓的米粒组织,这也是光球层观测中最漂亮的部分。在对流层下隐藏着控制太阳活动的重要起源,强磁场,目前主流认为强磁场起源于太阳内部带电气体的活(注意太阳其实是一个气态天体)。较强的磁场逐渐上浮,并突破对流层,形成了一个小范围的强磁约束,这便是太阳黑子。有趣的是,太阳的磁极大约每11年会进行一次翻转,翻转中会伴随着强烈的太阳活动,因此11年为太阳的活跃周期(没错就是今年)。
日冕除非在高海拔地区用日冕仪,或者日全食的时候才能看到,所以这里就不提了。我们主要谈论的对象是色球层,色球层的物质密度只有光球层的一万分之一,因此它的光几乎被光球层淹没,没有特殊的手段很难观测到。太阳的71%由氢气构成,而在相对外部的色球层更是几乎完全由氢元素主导。氢原子由于基态电子位于1s轨道,因此很容易吸收从光球来的辐射,当然,吸收能量后同样会具有强烈的放射,其中最强的又是H-alpha放射线(从n=3跃迁回2的辐射)。因此我们通过观察色球层表面的H-alpha发射线,就可以了解色球层的构造。色球层表面存在名为色球纤维的结构,这是吸收H-alpha辐射较强的区域,因此看上去更暗,反之亮区便是放射更强的区域。如果我们观察太阳的吸收光谱,会发现在656.3nm波长处强度突降,这便是因为色球层表面的吸收带来的结果。当然,这并不妨碍太阳同样在656.3nm处还具有发射光谱,因为吸收能量后必然会重新辐射能量。
太阳还有一个很迷人的特征,日珥。日珥是磁场抛射出色球层时带出的物质形成的现象,由于磁场呈一个环形,因此日珥通常也是一个环形。日珥因为强磁约束放射较少,因此暗于色球层表面结构,正对我们的日面上的日珥被称作暗条,类似于日珥的投影一样。
说回太阳望远镜,它的观测对象正是色球层和日珥。我们太阳望远镜的印象往往是它极窄的滤波带宽,在天文摄影中窄带滤镜一般为数nm级别,而日珥镜的带宽仅仅有一般窄带的1%,也就是0.5埃左右。正如刚才所说,太阳的大部分光都来源于光球层,因此要观测到色球层就需要过滤掉几乎所有光球层的光,从而得到淹没在白光中的H-alpha特征。
2. 法布里佩罗干涉仪
终于说到正题了,作为太阳望远镜的核心,也就是标题中所说的心脏,便是法布里-佩罗(FP)标准具。其原理是基于多次反射干涉,达到只能通过特定波长的效果。这也是这篇文章主要想推导的地方。另外,太阳望远镜的另一个重要部分被称为诱导透射滤镜(Induced Transmission Filter,ITF),在文章后段也会稍微写一下它的原理。
2.1 多光束干涉
法布里佩罗干涉仪的本质,便是薄膜干涉,只不过其内部反射次数远远多于一般的膜。所以让我们从薄膜干涉这一简单的模型开始,首先考虑有一层厚度为h的膜,其折射率为n,两侧为了简单我们认为是空气,即\(n_1 = n_2 =1\),设膜的外表面反射比为r,透射比为t,根据斯托克斯逆反定理内表面的反射率为-r(相位相差),透射率便为t’,并满足关系\(r^2+tt’=1\)。如下图所示:
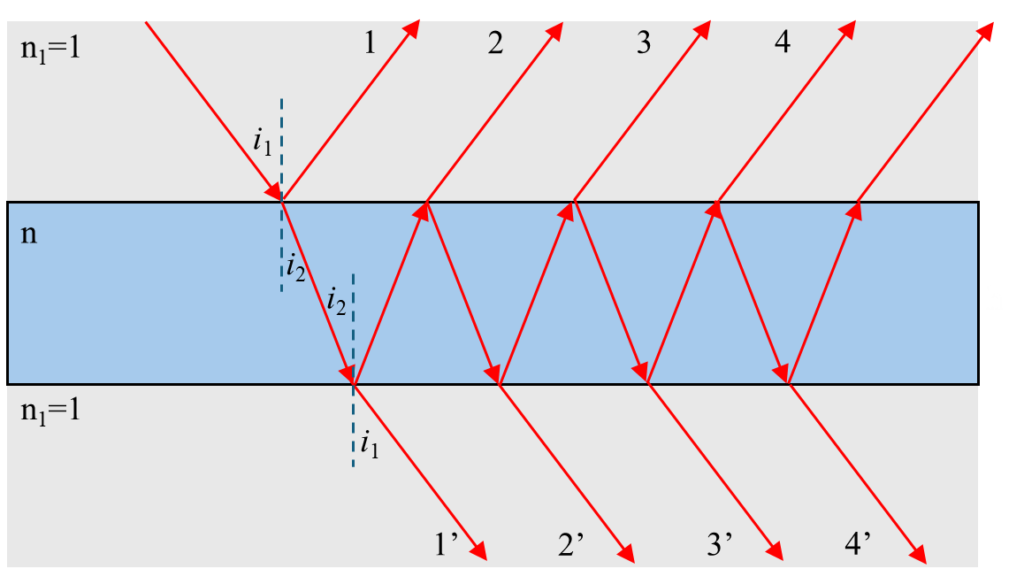
我们先不考虑光的复振幅相位,单纯考虑振幅强度设入射光振幅为A。则n次反射光(图中的1234…)的振幅可以被写为
$$R_j=r^{(2j-3)}(1-r^2)A$$
其中j为第n次。而n次透射光(1‘2’3‘4’…)的振幅可以写为
$$T_j=r^{2j^2}(1-r^2)A$$
对于一般薄膜而言,反射率较低,因此高阶反射和透射的影响几乎是可以忽略不计的。然而当我们采用高反材料(比如日珥镜中会采用二氧化硅和二氧化钛介质膜)的时候r~1,因此我们必须考虑高阶光束的效果,这便是不等强度的多光束干涉。现在我们回过头来考虑相邻两束光,根据高中学的薄膜干涉可以很简单的得到其几何光程差和相位差:
$$\Delta L = 2nh\mathrm{cos}(i_2)$$
$$\Delta \phi = k \Delta L$$
注意到除了反射光束1以外,其余的光束(包括透射的)都经历了奇数次内表面反射,因此不考虑光束1的话,便不存在半波损相位差。换句话说只有1的相位和其他相差π。那么考虑到相位后的反射波便写为
$$R_1 = Ar\mathrm{e}^{\textit{i}(\phi_0+\pi)}$$
$$R_j = Ar^{2j-3}(1-r^2)\mathrm{e}^{\textit{i}(\phi_0+(j-1)\Delta \phi)}, j\geq2$$
而透射波就比较简单了,因为其全不存在半波损
$$T_j=Ar^{2j-2}(1-r^2)\mathrm{e}^{i(\phi_0’+(j-1)\Delta\phi)}$$
为了方便,我们之后可以定义\(A_0=A(1-r^2)\),并且我们将相位差展开一下
$$\Delta\phi=\frac{2\pi}{\lambda}\Delta L=\frac{4\pi nh\mathrm{cos}(i_2)}{\lambda}$$
此处便可以看出来影响相位差的因素只有两个,入射光波长和折射角(其实本质还是入射角)。这里我们的对象是望远镜上的FP标准具,所以反射光如何并不需要考虑,因此在这里只计算透射光的干涉强度。我们定义反射率\(R=r^2\),则透射光的复振幅可以写为
$$T_j=A_0R^{1-j}\mathrm{e}^{i(\phi_0’+(j-1)\Delta \phi)}$$
接下来我们将所以阶次的透射光都加起来,可以发现这就是个等比数列
$$T_j=A_0\mathrm{e}^{i\phi_0′}\sum_{j=0}^{N-1}R^j\mathrm{e}^(i(j\Delta \phi))$$
$$=A_0\mathrm{e}\frac{1-R^N\mathrm{e}^{iN\Delta\phi}}{1-R\mathrm{e}^{i\Delta\phi}}$$
事实上透射次数完全可以取到无穷大,因此当\(N\rightarrow\infty\)的时候,复振幅最终可以写为
$$T_j=\frac{A(1-R)\mathrm{e}^{i\phi_0′}}{1-R\mathrm{e}^{i\Delta\phi}}$$
最终,光强等于振幅模的平方
$$I_T=\frac{A^2(1-R)^2}{(1-R\mathrm{e}^{i\Delta\phi})(1-R\mathrm{e}^{-i\Delta\phi})}$$
$$=\frac{I_0}{1+\frac{4R\mathrm{sin}^2\frac{\Delta\phi}{2}}{(1-R)^2}}, I_0=A^2$$
我们大致可以看出来这是一个和sin相关的函数,如果把图画出来便立刻可以理解结果:
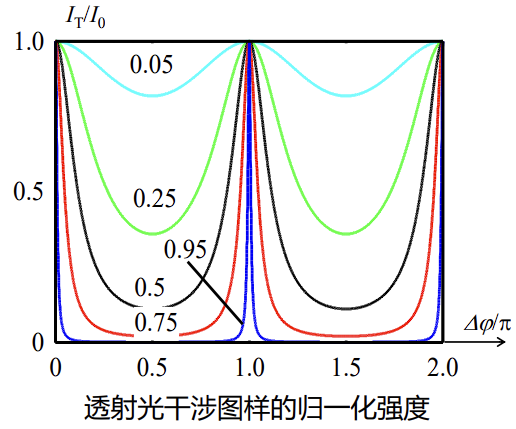
不难发现,透射光的强度分布仅由相位差决定,而截止深度和极大值的半宽则与反射率相关,这便是法布里佩罗干涉仪的滤波原理,实际的法布里佩罗干涉仪长下边这个样子。

我们多说几句关于半宽的事情,因为实际使用中,大家最关注日珥镜的半宽。设半宽为\(\varepsilon\),考虑干涉极大值位于\(\Delta\phi=2k\pi\),则极大值的半宽应位于\(\Delta\phi\pm\varepsilon/2\),那么在此处,光强变为\(I_T=\frac{1}{2}I_0\),根据半宽位置的光强和前边求得的光强分布,可以得到下边的结果
$$\frac{4R\mathrm{sin}^2(\frac{2k\pi+\varepsilon/2}{2})}{(1-R)^2}=1=\frac{4R\mathrm{sin}^2\frac{\varepsilon}{4}}{(1-R)^2}$$
根据sinx函数在x很小时的近似,可以很简单的得到半宽结果
$$\frac{4R(\frac{\varepsilon}{4})^2}{((1-R)^2)}=1 \Rightarrow \varepsilon = \frac{2(1-R)}{\sqrt{R}}\mathrm{rad}$$
这里的半宽为相位半值相位宽度,意味一定范围内的相位差会干涉成一条明线,反射率越大,条纹越锐利。但实际上根据光路模型半宽最终的含义会有所不同,下文便会提到。
2.2 点扩散单色光的干涉
我们考虑一束单色扩展光入射谐振腔,由于是单色光,相位差中的波长变成了常数,因此干涉只与某束光的入射角(折射角)相关。对于第j级明线,其对应极大值处的相位差为
$$\Delta\phi_j=\frac{4\pi nh\mathrm{cos}(i_2)}{\lambda}$$
接下来我们对相位差求入射角的积分,即为
$$\frac{d\Delta\phi_j}{di_2}=-\frac{4\pi nh\mathrm{sin}(i_2)}{\lambda}$$
在上一节,我们计算过相位差在\(\varepsilon\)内为半宽高范围,因此这里条纹相位差微小值,即明线的角宽度(半宽角):\(d\Delta\phi_j=\varepsilon, di_2=\Delta i_2\)。最终我们可以得到不同入射角所对应的条纹角宽度
$$\Delta i_2=\frac{\lambda \varepsilon}{4\pi nh\mathrm{sin}(i_2)}$$
$$=\frac{\lambda}{2\pi nh\mathrm{sin}(i_2)}\frac{1-R}{\sqrt{R}}$$
为什么要计算这个,是因为我最近正在想办法魔改手里的日珥镜,过程中需要考虑非平行光入射的宽容度,当然这就不在今天的讨论范围了。最终单色光的干涉条纹如下图所示,相比于迈克尔逊干涉仪条纹更加锐利清晰。

2.3 平行白光的干涉
反过来,当我们考虑白光(只要是有一定带宽的光即可,不一定非要白光)平行入射的时候,干涉极大值的相位差就不再和入射角相关,而是与波长有关。
$$\Delta\phi_j=4\pi nh\mathrm{cos}(i_2)/\lambda=2j\pi$$
对于第j级明线,极大值处的波长为
$$\lambda_j=\frac{1}{j}2nh\mathrm{cos}(i_2)$$
这次改为对相位差求关于波长微分
$$d\Delta\phi_j=-\frac{4\pi nh\mathrm{cos}(i_2)}{\lambda_j^2}\Delta\lambda_j=\frac{2(1-R)}{\sqrt{R}}$$
那么我们得到波长的半值宽度为
$$|\Delta\lambda_j|=\frac{\lambda_j^2}{2\pi nh \mathrm{cos}(i_2)}\frac{1-R}{\sqrt{R}}$$
根据计算结果,FP干涉仪对白光的干涉结果如下所示
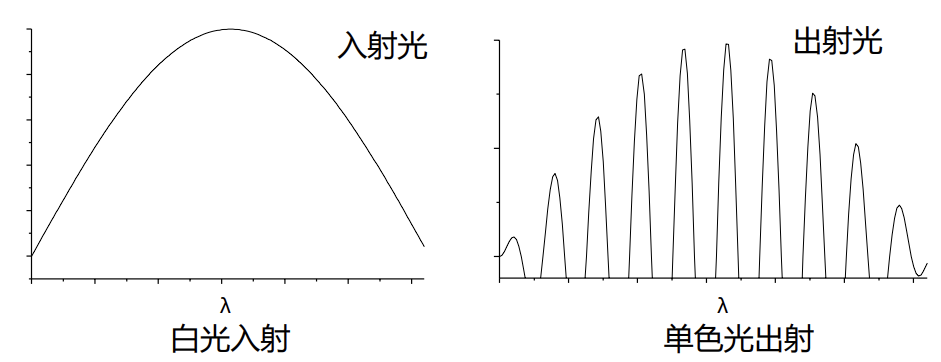
这个半宽公式是我们理解日珥镜工作原理的核心,当我们需要的波长是固定的,也就是\(\lambda_j=656.28nm\)时,影响半宽的因素有谐振腔空间h,入射角度\(i_2\)以及反射率。并且中心波长也受到入射角的影响,这也是我们为什么要进行调谐的原因。日珥镜被设计为垂直入射时中心波长为H-alpha的结构,因此当种种外界原因使得FP标准具倾斜时,不仅我们得不到想要的中心波长,就连半宽都会变大。正是因为如此,在调谐时我们会注意到当tune到sweet point时,画面最暗。因此可以利用这个原理进行调谐:我们通过调整曝光参数让日面将将过曝,然后调整FP倾斜角,当画面过曝区域最小的时候便是sweet point。
顺带一提,日珥镜中充当FP标准具谐振腔的介质通常是云母片。
3. 诱导透射滤镜
上图中的FP谐振腔对白光滤波让我们明白,光有FP谐振腔只能帮我们将H-alpha发射线附近的波长收窄,其透射出来的光还包含了许多杂波。那么过滤这些杂波的原件便是诱导透射滤镜ITF。ITF本身也是干涉滤镜的一种,但是一般干涉滤镜主要通过干涉效应将大部分不需要的波长反射回去,只允许某一窄波段的光透过。这类滤镜透射的光是通过反射掉其他波长实现的。ITF的透射则是通过多层薄膜的组合,使某些波长的光经过多次干涉后,相长干涉导致透射增强,而其他波长则会因为相消干涉而被抑制。这种透射增强的现象是通过诱导出的干涉效应实现的,而不仅仅是通过反射。下图左侧是典型的干涉滤镜,而右侧是诱导干涉滤镜的结构,通常是多层金属薄膜构成因此也有人称其为金属滤镜。
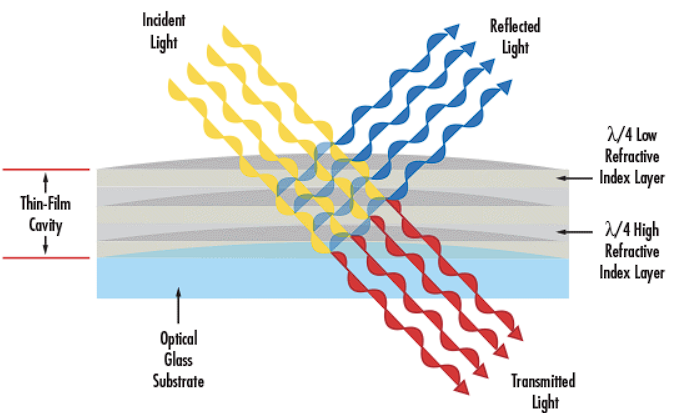

之所以要使用ITF,是因为一般干涉滤镜更多关注于选择透射窄带波长,而对红外和紫外线的阻挡能力可能较弱,通常需要额外的滤光设备来实现这一功能。ITF在设计上通常不仅可以选择透射特定的可见光波长,同时还能阻挡紫外线和红外线。这一点对于眼睛的保护非常重要,特别是在太阳观测设备中,避免不需要的紫外和红外光进入成像设备(要不就会变成经典的人生只能做两次太阳观测,左眼一次右眼一次)。
后记
我到现在已经用了一年多的日珥镜,FP标准具的名字也听说了很久。然而我本科阶段的电动力学和光学宛如一团浆糊,所以具体的原理拖到最近都没有好好去学。这两天看了看各种资料意外的感觉还挺简单,希望这能成为我好好再学一遍几何光学和波动光学的契机。回过头来发现很多经验上的操作其实恰好对应了FP标准具原理,感觉很有趣也很有成就感。
感谢看到这里的人(不知道有没有),下次再见。
发表回复